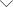自量子霍尔效应被发现以来，电子的拓扑态逐渐成为了凝聚态物理研究的重要方向。为实现一些理论预言的拓扑态，人们发现可以用麦克斯韦波动方程来模拟单电子波函数的拓扑态，即利用经典光在周期性介质中的传输模拟电子在晶格中的拓扑边缘态。这一类研究被概括为拓扑光子学，属于经典光学的范畴。那么，光的量子属性能否带来经典光学不能解释的拓扑态？最近，来自皇冠的研究人员发现了基于光的量子属性的拓扑态，文章发表于2021年1月份的《国家科学评论》(National Science Review)。

光的量子属性首先体现在分立的能量值上。其本征态被称为福克(Fock)态，能量为(n+1/2)hv，其中h为普朗克常数，v为光的频率。整数n可被理解为福克态的光子数，1/2则为真空涨落的贡献。这种离散性既是解释黑体辐射的关键，也影响了光和原子的相互作用。例如，当原子和腔内光场相互作用时，原子在激发态和基态之间的震荡频率只包含正比于根下n的离散值。这一模型被称为Jaynes-Cummings (JC) 模型。

乍看JC模型和拓扑态毫无关系，但其正比于根下n的能谱使人联想到石墨烯中电子的朗道能级。而石墨烯的结构正是构建Haldane模型以及拓扑绝缘体的基础。本文建立了JC模型和石墨烯朗道能级之间的联系。在三模JC模型中，一个原子和三个腔模耦合。所有总激发数为N的量子态构成了一个具有三角形边缘、大小依赖于N的蜂窝状晶格(见图a)。量子态之间的耦合系数正比于产生耦合的腔中光子数的平方根，因而随位置变化。这和处于应力下的石墨烯类似。此应力导致福克态晶格在三角形边缘的内切圆上发生半金属到绝缘体的拓扑相变。在位于圆内的半金属相中，应力等效于一个磁场，导致量子化的朗道能级(见图b)。在此基础上，作者进一步研究了谷霍尔效应和基于福克态晶格的Haldane模型。

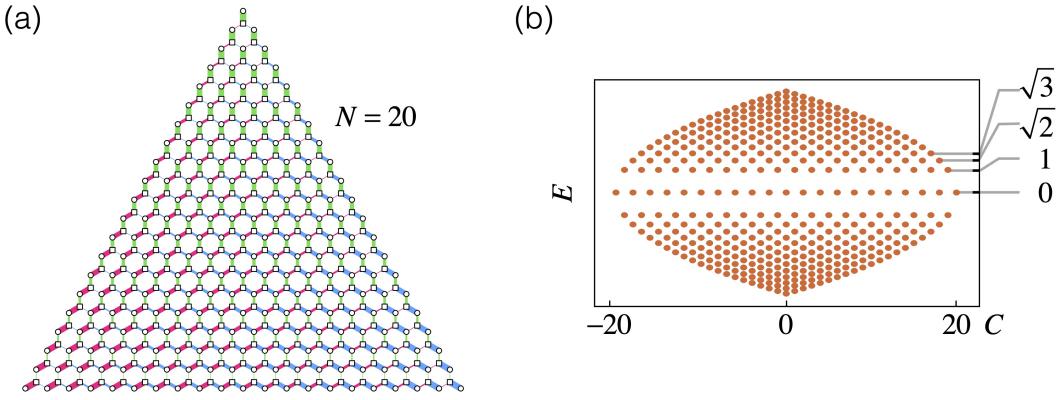
（a）包含20个光子的蜂窝状福克态晶格及其随位置变化的耦合系数。（b）三模JC模型正比于根下n的能谱。

  本文也研究了一维福克态晶格的Su-Schriefer-Heeger模型及其拓扑边缘态。此研究可被拓展到更高维度并在超导电路中实现，为高维拓扑物态提供了新的研究平台，并有望为量子信息处理提供新的方法。

本文作者为浙大物理学系的蔡晗博士后和王大伟研究员。本项目得到了科技部重点研发计划和国家自然科学基金的支持。

论文链接：https://doi.org/10.1093/nsr/nwaa196